1T-Lineære ulikheter. Fortegnslinjer

Vi starter nå et nytt kapittel som har fått navnet Grafer og ulikheter. Vi går da et stykke videre i forhold til det vi lærte i algebra tidligere i år. Vi har allerede lært å løse forskjellige ligninger, men nå møter vi ulikhetene. Vi kan behandle ulikhetene som vi behandler ligninger, men det er noen viktige forskjeller. Er vi ikke oppmerksomme på disse forskjellene, kan løsningene våre bli uriktige.

Det er ialt 4 videoer knyttet til dette emnet. Jeg gjør oppmerksom på at dette var de første videoen for undervisningsbruk som jeg laget. I dag lager jeg videoer på en annen måte. Matematikken som vi går igjennom, kan du likevel stole du. De to første videoene bør du se i rekkefølge. Her går vi går vi blant annet igjennom de forskjellige ulikhetstegnene. Det er viktig at du forstår forskjellene mellom likhetstegnet og ulikhetstegnene. Du finner videoene ved å gå inn på video 1 og video 2.

Når du har sett disse videoen, skal vi lære hvordan vi løses enkle lineære ulikheter. Videoen tilknyttet dette emnet finner du her. Det er sikkert lurt å prøve å løse noen slike ligninger rett etter at du har sett videoen. Både oppgave 7.1 og 7.30 er her alternativer.

Et viktig redskap når vi arbeider med ulikheter, er fortegnslinjer. Videon tilknyttet dette emnet finner du her . Prøv også å tegne noen fortegnslinjer når du har sett videoen. Se oppgaver på arbeidsplanen.

Hvis du har fått gjort alt dette til neste time, kan du være godt fornøyd med arbeidsinnsatsen.

1T- En oppgave. To løsninger

Videoen tilknyttet dette temaet finner du her. Du finner notatene om du åpner linken notater.

Dette innlegget er ikke ferdig ennå, men linkene ovenfor kan brukes. Lykke til !

1T-Bevis tre setninger i trigonometri

Videoen som er tilknyttet dette emnet finner du ved å gå her. Notatene som jeg har brukt, kan du studere om du går inn på notater.

Først i denne videoen gikk vi i gjennom tre definisjoner: Supplementvinkler, komplementvinkler og motsatte (omvendte ) vinkler. Du fikk også noen oppgaver å løse tilknyttet disse definisjonene. Bakgrunnen for dette er todelt.

1. Det å arbeide med definisjonene gjør at vi lettere lærer definisjonen. Definisjoner må bare læres. De er som gloser når du lærer engelsk. Det blir helt håpløst å snakke engelsk hvis du ikke kan noen engelske ord. 
2. Du skal forstå og lære setningene som er tilknyttet hver av disse definisjonene. 

Dette vil du få bruk for i mange sammenhenger, så dess raskere du lærer deg disse definisjonene med medfølgende setninger, dess lettere blir det løse oppgaver. Vi får egentlig ikke brukt disse setningene når vi beviser setningene, men i stoffet som kommer i neste video, blir dette høyst aktuelt.

Bevisene er av forskjellig vanskelighetsgrad. Jeg gjennomfører bevisene slik at vi gjør det enkleste først. Å bevise cosinussetningen er nok det vanskeligste. Du må ikke regne med at du skal forstå alle bevisene med en gang. Derfor bør du studere dem flere ganger, både med video og uten video.

1T-Areal-, sinus- og cosinussetingen

Videoen tilknyttet denne videoen finner du ved å gå inn på denne linken. Notatene som jeg brukte under produksjonen kan du studere om du åpner notater. Du bør se videoen og studere notatene før du går videre på teksten under.

Dette kapitlet dreier seg egentlig om disse tre setningene. I videoen har jeg vist noen av de anvendelse som disse setningene har. I de eksemplene som jeg viste, kunne vi bruke setningene uten å tenke oss så mye om. Merk deg følgende om disse oppgavene:

1. Alle vinklene var spisse, altså mellom 0° og 90°. Blant annet kunne vi se det greit fra figurene fordi forholdene mellom alle sidene var tegnet nøyaktig. Det kan bli annerledes hvis én vinkel er stump, altså mellom 90° og 180°. 
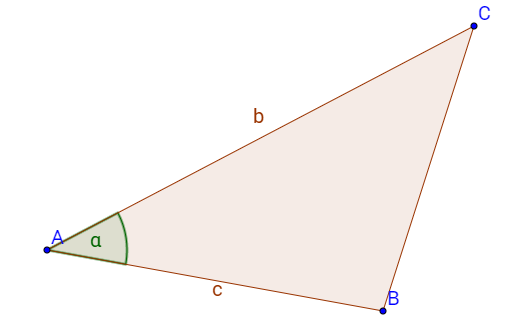
2. Hvis vi en trekant har fått oppgitt lengden av to av sidene og den mellomliggende vinkelen mellom disse sidene, er vi helt trygge. Se trekanten under:

I denne trekanten  kjenner vi sidene AB og AC. De har henholdsvis lengden c og b. Den  mellomliggende vinkelen til sidene AC og AB, er vinkelen som vi markert. I en slik situasjon er alt bestemt. Vi kan både bruke arealsetningen, sinussetningen og cosinussetningen med vellykket resultat. Det blir helt annerledes om vi fikk oppgitt de samme sidene, men én av de andre vinklene. 

Noen ganger kan en oppgavebeskrivelse gi to løsninger. Det skal vi nærmere på i videoen "En oppgave. To løsninger". Det gjelder å kjenne igjen situasjoner når vi er helt trygg, og situasjoner der vi kan få flere løsninger.

1T-Enhetssirkelen

Videoen som er tilknyttet dette emnet finner du ved å gå inn her

Notatene som jeg har brukt da jeg lagde videoen finner du ved å gå inn på notater.

Her finner du linken til geogebra-filen med enhetssirkelen: Enhetssirkelen. Bruk enhetssirkelen til å finne sinus og cosinus til følgende vinkler: 0°, 50°, 80°, 115°, 155°, 220°, 330°.

Hvis du har skjønt hvordan enhetssirkelen fungerer, vil du klare å fylle ut skjemaet som du finner ved å gå inn her. Dette er stoff som du bør beherske og som du derfor vil bli testet om du kan. 

I videoen har vi i realiteten løst oppgave 6.3 og 6.4. Du vil ha løst oppgave 6.13 når du fylt ut skjemaet ovenfor. 

Du skulle nå være rustet til å gå i gang med alle oppgaver som du finner i oppslagene 6.1- 6.4. Løs oppgavene 6.1-6.19 først.

Lykke til!

1T- Innledning om trigonometri

Endelig har jeg fått komme i gang igjen og produsere nye undervisningsvideoer. Videoen til dette emnet finner du om du går inn på linken her. Notatene som jeg brukte da jeg lagde videoen finner du om du går inn på notater. Du bør se videoen, før du går videre i denne teksten.

Som du har sett, startet vi med å oppsummere hva vi vet om trekanter fra før. Det meste av det du kan om trekanter, lærte du i grunnskolen, men noe har du nok lært i løpet av dette første året i videregående skole. Ikke minst har vi brukt tid på repetere stoff som du har vært borti før. Derfor er nok forståelsen din for stoffet betydelig høyere enn det den var da du startet her hos oss.

Det er som regel klokt å gjøre slike oppsummeringer før en starter med nytt stoff. Det bør du derfor selv gjøre til en vane.

Trigonometrien hviler på tre definisjoner:

Vi setter ofte opp ligninger når vi skal løse den type oppgaver som vi møter i dette videoen. Det må du også gjøre når du kommer til oppgavene i læreboka. Da gjelder det at du løser disse ligningene riktig. Husk da på skålvekta som vi har tatt fram i mange sammenhenger. 

Lykke til !