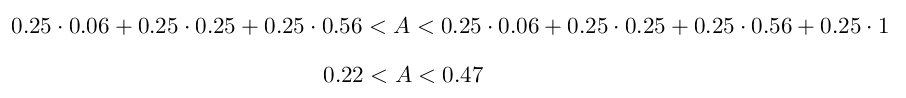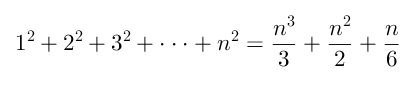1T-Kvadratsetningene

Videoen tilknyttet denne teksten finner du ved å gå inn her. Du bør se videoen før du  leser videre på denne teksten. Notatene som jeg brukte i videoen finner du ved å gå inn på på notater.

Som du kan observere, begynner vi dette kapitlet på en litt uvanlig måte. Vi starter ikke med oppslag 5.1 Tallmengder, Intervaller som en kanskje kunne forvente. Derimot går vi rett på en svært praktisk oppgave. Det er en fordel om du har sett videoen og forberedt deg litt før du kommer på skolen. I timen vil dere få utlevert papir og sakser. Skrivesaker regner jeg med at dere har selv.

Resten blir problemløsning, og dere må regne med at ikke alt er like enkelt. Husk at dette skal løses praktisk. Det er ved å klippe eller brette, at dere kommer fram til løsningene.

R2-Integrasjonsteknikker

Videoen som er tilknyttet denne teksten, finner du om du går inn her.
Notatene som jeg brukte i videoen finner du om du åpner notater.
Denne teksten er ikke ferdig, men publiseres slik at du kan nå disse to linkene.

TScB-Vurdering av en sykdomstest

1T-Union. Addisjonssetningen

Videoen tilknyttet dette innlegget finner du her. Du finner notatene som er brukt i videoen om du åpner notater.

Denne teksten er ikke ferdig, men er åpnet slik at du skal ha tilgang til linkene.

1T-Disjunkte hendinger. Total sannsynlighet

Videoen tilknyttet dette innlegget finner du her. Du bør se videoen for å ha fullt utbytte av denne teksten. Notatene som jeg bruker i videoen finner du når du åpner notater.

Denne teksten er ikke ferdig, men er likevel åpnet fordi den gir linkene som du trenger for å arbeide med stoffet

1T-Venndiagram

Videoen tilknyttet dette innlegget finner du her. Du bør se videoen for å ha fullt utbytte av denne teksten. Notatene som jeg brukte i videoen, finner du om du åpner linken notater.

Venndiagram er et svært nyttig redskap for å løse flere typer problemstillinger innenfor sannsynlighetsregning. Jeg vurderer det ikke som spesielt vanskelig. Jeg har erfart at alle elever som legger inn en skikkelig innsats, lykkes med å beherske dette stoffet.

Det trenges trening for å bli flink til å sette opp slike diagrammer, så her er det ikke nok å se på at andre løser slike oppgaver. Du må gå i gang selv. Det er viktig å trene både med og uten bok. Det er helt sikkert at du vil møte slike oppgaver en rekke ganger. Dess mer du har trent, dess større er muligheten for å lykkes.

TScB-Fødseldagsproblemet

1T-Komplement. Sannsynligheten for minst én

Videoen tilknyttet dette innlegget finner du her. Du bør se videoen for å ha fullt utbytte av denne teksten.
Notatene som jeg brukte i videoen finner du om du åpner linken notater.

Når en har skjønt det stoffet som vi går igjennom i denne videoen, har en kommet langt. Ikke alt dette er så lett tilgjengelig, og du må regne med å bruke noe tid.

Jeg stiller i alt tre spørsmål i videoen som du utfordres til å finne svar på. De refereres muntlig i videoen, men går du inn i notatene, finner du også spørsmålene der. De to første skulle ikke være så vanskelige, men fødselsdagsproblemet er en utfordring. Her finner du en link til fødselsdagsproblemet: Fødselsdagsproblemet

De to første spørsmålene, vil vi snakke om i førstkommende time. Det finnes mange grader av svar. Det mest grunnleggende er at en kan referere spørsmålet.

Lykke til!

R2-Regneregler for integrasjon. Areal mellom grafer. Samlet mengde

Videoen tilknyttet denne overskriften finner du her. Du bør se videoen for å få fullt utbytte av denne teksten.


Det er tre setninger tilknyttet funksjonene f(x) og F(x), og g(x) og G(x)  som står sentralt i denne videoen. Det er følgende sammenheng mellom disse funksjonene:

     

Da gjelder følgende regneregler:

Det er en fjerde setning, som vi allerede har brukt, og som vi vil komme tilbake til igjen og igjen. Denne bør du også lære deg og forstå. Det er:

Du kan sjekke ut denne setningen ved å se på følgende eksempel:

1T-Snitt mellom hendinger. Produktsetningen

Videoen tilknyttet denne overskriften finner du på her. Du bør se videoen for å ha utbytte av denne teksten.

I forrige oppslag arbeidet vi betingede sannsynligheter og uavhengige/avhengige hendinger. Dette stoffet får du  bruk for her. Hvordan avgjør vi om to hendinger er uavhengige? Spørsmålet har et helt presist svar som vi nå kan repetere:

I videoen får du en del oppgaver som du skal arbeide med. Du finner dokumentet som jeg brukte og opgavene om du går inn på denne linken. 

Mine løsninger på oppgaven finner du her, men denne siden åpner jeg ikke ikke før etter at dere har arbeidet en stund med oppgavene. 

Lykke til med oppgaveløsningen

R2-Mer om integraler og arealer

Videoen tilknyttet til dette innlegget finner du her. Du bør se videoen for å ha fullt utbytte av denne teksten.

Da vi innledet dette kapitlet, studerte vi sammenhengen mellom integraler og arealer. Ofte kan vi sette likhetstegn mellom integraler og arealer, men ikke alltid. Måler vi et areal, er størrelsen alltid større eller lik null. Integraler kan kan derimot både være positiv, negative og lik null. Det avgjørende er om grafen til kurven er over eller under x-aksen slik vi ser i denne videoen.

Når vi skal beregne arealer mellom grafen og x-aksen, må vi derfor ta hensyn  til om grafen ligger over og under x-aksen. Eksemplet med sin(x) viser dette med all tydelighet. Når vi får oppgave der vi skal beregne arealer mellom en grafen og x-aksen, vil det ofte være tjenlig å finne nullpunktene til funksjonen.

De integralene som vi skal løse i dette oppslaget, kan vi løse raskt hvis vi kjenner de antideriverte til de grunnleggende funksjonene. Jeg tenker da særlig på funksjonene som du finner på denne listen:

 På det nivået som vi er, er det å kunne dette listen den viktigste forutsetningen for å få suksess. Mer avansert intervallregning blir ytterst vanskelig hvis ikke disse antideriverte er i korttidsminnet.

1T-Betinget sannsynlighet. Uavhengige og avhengige hendinger.

La A og B være to hendinger.
P(A|B) betyr at det er lagt inn en betingelse for at A skal være oppfylt. B er betingelsen. P(A|B) er altså den betingede betingelse for at A er oppfylt.

Jeg har erfaring med at dette stoffet fortoner seg vanskelig for mange elever. Vanskelighetene blir betydelig mindre hvis en lærer seg å spørre. Hva er betingelsen?

Tabellen over viser den ferdig utfylte krysstabellen i oppgave 4.15. Det viste seg å være lurt å fylle den ut. Generelt gjelder at krysstabeller er et egnet redskap når vi arbeider med betingede sannsynligheter.

P(S|G) leser vi "P av S gitt B". Her er G betingelsen. Vi skal altså finne ut hva sannsynligheten er for at en gutt har mp3-spiller.

Vi har en intuitiv, språklig forståelse av hva det betyr om to hendinger er avhengige av hverandre eller uavhengige. I matematikk er ikke dette tilstrekkelig. Vi trenger en mer presis definisjon. Hvis vi skal avgjøre om S og G er uavhengige, må følgende spørsmål besvares:

Er P(S)=P(S|G)? 

Er svaret Ja, er hendelsene uavhengige. Er svaret nei, er det avhengige.

Her nytter det altså ikke med synsing. I svaret på et enkelt spørsmål, finner vi løsningen.

1T- Store talls lov

Store talls lov 

"Når vi gjentar et forsøk nok mange ganger, vil den relative frekvensen for et utfall nærme seg sannsynligheten for utfallet "

Dette er formuleringen  av  de store talls lov som læreboka bruker. I videoen, som du finner ved å åpne den følgende linken, vil du lære mer om hva denne loven går ut på.

Store talls lov virker sterkere og sterkere dess flere repetisjoner vi gjør av et forsøk. Dette har vi fått erfare ved å gjøre mange terningkast og samle dem i et eget regneark. Du kan åpne regnearket her. Sammenlign de relativ frekvensene som du oppnådde ved 100 repetisjoner med de relative frekvensene for hele klassen. Observerer du noen effekt av store talls lov?

Vi lærer i videoen hvordan vi kan simulere terningkast. Denne formelen kan du bruke for å simulure et terningskast: =TILFELDIGMELLOM(1,6). Skal du telle antall 2-ere, innenfor et område kan vi bruke kommandoen =ANTALL.HVIS(A3:A12;2). Hvis vi skal kopiere formelen til andre ruter, må vi bruke et dollartegn: $. Da blir formelen =ANTALL.HVIS($A$3:$A$12;2).

Fordelen med å simulere, er at vi kan få kastet mange flere kast på mye kortere tid enn om vi fysisk skulle gjøre det. Det kan være en nyttig øvelse å eksperimentere med dette.

1T-Illustrasjon av utvalgsrom

Videoen med denne tittelen finner du her. Du bør se i gjennom videoen før du leser denne teksten.

Utallige ganger har jeg, rett er at en oppgave et gitt, fått følgende spørsmål fra elever:

"Jeg forstår ikke denne oppgaven. Kan du hjelpe meg?" 

Jeg har mange ganger vært fristet til å svare: "Det gjør ikke jeg heller", og  det ville vært helt sant i mange tilfeller.  Mange oppgaver jeg forstår jeg ikke bare ved å lese teksten. Skal jeg løse makte å løse oppgaven, trenger jeg  en illustrasjon, men når illustrasjonen er ferdig, er oppgaven ofte så godt som løst.

I de oppgavene vi arbeider med i denne videoen, blir dette poenget godt illustrert. Lærer vi å bruke enkle redskaper som valgtre, krysstabell, diagrammer og oppramsinger, går oppgavene raskt fra å være uløselige eller vanskelige til å bli enkle. Vi må trene på slike teknikker for å bli flinke. Det er ikke noe annet å gjøre enn å løse mange oppgaver. Prøv gjerne å løse oppgavene uten å se på et eksempel eller løsning av en annen oppgave.

Oppgave 4.7 står igjen til deg. Ser du på ett av eksemplene, kan det være til stor hjelp. Oppgave 4.9 skal vi løse i forbindelse med en time.

Gi deg ikke med å løse de oppgavene som vi har løst sammen. Prøv deg på ukjente oppgaver som du finner bak i læreboka. Du kan være sikker på at ett av hjelpmidlene  oppramsing, krysstabell, diagrammer eller valgtre, vil forvandle oppgaven du strever med fra uforståelig og vanskelige til forståelige og løsbare.

   

R2-Algebraens fundamentalteorem

Videoen knyttet til dette emnet finner du her. Du bør se videoen før du leser denne teksten.

Algebraens fundamentalteorem er et av de viktigste teoremene(setningene) i matematikken. Det kobler sammen integralregning og derivasjon, og gjør at det å finne integraler blir mye enklere. Jeg markerer, i motsetning til læreboka,  betydningen av setningen  ved å benevne setningen med sitt egentlige navn. Navnet i seg selv forteller om betydningen som setningen har.

Min video bygger i hovedsak på Tom Lindstrøms bok Kalkulus, Universitetsforlaget 1996. Vi gjennomfører ikke et fullstendig bevis av setningen, men vi kommer et langt stykke på vei. Hvis du har lyst til å studere et fullstendig bevis av setningen, viser jeg til Lindstrøms bok.

Mine videoer dekker nå de tre første oppslagene av av dette kapitlet. Det er viktig at du får løst mange oppgaver. Listen over antideriverte er det svært viktig å memorere så raskt som mulig. Ganske raskt vil du måtte bruke disse funksjonene for å integrere nye og mer sammensatte funksjoner, og da vil du slite hvis ikke disse antideriverte er på plass.

R2-Bestemt integral

Videoen knyttet til dette emnet finner du her, og du bør se videoen før du går videre på denne teksten.

I denne videoen fortsetter vi å nærme oss integralbegrepet ved å bruke Oversummer og Undersummer. Her er GeoGebra er svært redskap fordi vi kan observere hva som skjer med oversummene og undersummene når vi øker antall rektangler over og  under funksjonsgrafen:

På figuren under har vi valgt n=4. Det betyr at vi får fram 4 par av rektangler. Forskjellen mellom Oversum og Undersum er her på 0.25.
Vi har brukt kommandoene SumOver[f,0,1,4] og SumUnder[f,0,1,4] for å fram disse rektanglene:



Setter er n=75, vil forskjellen bli mye mindre, bare 0.1. Det er vist på figuren under. Her har vi brukt kommandoene SumOver[f,0,1,75] og SumUnder[f,0,1,75]:


For å regne ut integralet direkte, bruker vi kommandoen Integral[f,0,1,4]. Bestemte integraler har en nedre og øvre grense. Dette skriver vi slik:

Vi får nå snart lønn for det møysommelige arbeidet vi har gjort så langt. Vi er svært nær en dypere forståelse av hva integral er for noe. Før vi kommer dit, er det viktig at du skaffer deg erfaring med å beregne oversummer og undersummer. Dette skal du både beherske ved å bruke håndredskaper og ved å bruke digitale hjelpemidler. Faren ved å bruke digitale hjelpemidler med en gang, er at resultatene kommer så enkelt og rakst at vi ikke får tid til å reflektere over det vi ser. Derfor bør du tvinge deg selv til mye håndarbeid.

Lykke til !

R2-Innledning om integrasjon

Videoen Innledning til integrasjon finner du ved å åpne linken her. Du bør helst se videoen før du leser videre på denne bloggen.

Det er mulig å lære seg å integrere uten å skjønne så mye av det som foregår. Det handler om å kunne anvende noen regler og vite når en skal bruke dem. Det kan gå riktig bra en god stund, men i lengden blir en slik tilnærming til emnet utilstrekkelig. Det vil  føre til at det blir svært begrenset hvilke oppgaver en makter å løse.

I vår gjennomgang vil vi starte helt fra grunnen. Dypest sett handler integrasjon om å finne arealer. Vi tar utgangspunkt i hvordan vi lærte å regne ut arealet av enkle figurer som rektangel, trapes, parallellogram og sirkel. Vi forsøker så å bygge en bro fra denne type arealberegninger og til integralregningen. Som en vil se, er ikke spennet så langt.

Vi ønsker å finner arealet under funksjonen

.

På figuren under, som er den samme figur som ble brukt i videoen, har vi tegnet inn funksjonen. Vi finner tilnærminger til det aktuelle arealet ved enten å la arealet A bli omsluttet av fire røde rektanglet eller ved å la arealet A omslutte tre blå rektangler, se figuren.  Både summen av de røde rektanglene og summen av de blå rektanglene, kan brukes som estimat for arealet under kurven.  Summen av de tre blå rektanglene er 0.22 og summen av de fire røde rektanglene er 0.47.

Det er også instruktivt å sette opp hele ulikheten:

Antar vi så at arealet A ligger omtrent midt mellom disse to verdiene, vil A være tilnærmet lik 0.34. Dette viser seg å være et godt estimat. 

Siste del av videoen er krevende stoff. Vi generaliserer det vi gjorde ovenfor. I stedet for å dele i 4 deler, deler vi i n deler. Etter noe algebra kommer vi fram til uttrykket

(Gjør gjerne den samme utledningen, og sjekk om du får samme resultat.) 

Dette uttrykket kan forenkles enda mer ved å bruke identiteten 

Vi får da at 

Når n blir stor, hva vil A nærme seg?

Å beregne arealet A på denne måten, er ganske arbeidskrevende. Vi vil gjerne finne en raskere måte å komme fram til resultatene på. Metoden finnes, og det er dette som er integrasjon. Det arbeidet vi har gjort nå, er på ingen måte nytteløst. Det er slike betraktninger  som ligger til grunn for all integrasjonsregning.