Det er mulig å lære seg å integrere uten å skjønne så mye av det som foregår. Det handler om å kunne anvende noen regler og vite når en skal bruke dem. Det kan gå riktig bra en god stund, men i lengden blir en slik tilnærming til emnet utilstrekkelig. Det vil føre til at det blir svært begrenset hvilke oppgaver en makter å løse.
I vår gjennomgang vil vi starte helt fra grunnen. Dypest sett handler integrasjon om å finne arealer. Vi tar utgangspunkt i hvordan vi lærte å regne ut arealet av enkle figurer som rektangel, trapes, parallellogram og sirkel. Vi forsøker så å bygge en bro fra denne type arealberegninger og til integralregningen. Som en vil se, er ikke spennet så langt.
Vi ønsker å finner arealet under funksjonen
.
På figuren under, som er den samme figur som ble brukt i videoen, har vi tegnet inn funksjonen. Vi finner tilnærminger til det aktuelle arealet ved enten å la arealet A bli omsluttet av fire røde rektanglet eller ved å la arealet A omslutte tre blå rektangler, se figuren. Både summen av de røde rektanglene og summen av de blå rektanglene, kan brukes som estimat for arealet under kurven. Summen av de tre blå rektanglene er 0.22 og summen av de fire røde rektanglene er 0.47.
Det er også instruktivt å sette opp hele ulikheten:
Antar vi så at arealet A ligger omtrent midt mellom disse to verdiene, vil A være tilnærmet lik 0.34. Dette viser seg å være et godt estimat.
Siste del av videoen er krevende stoff. Vi generaliserer det vi gjorde ovenfor. I stedet for å dele i 4 deler, deler vi i n deler. Etter noe algebra kommer vi fram til uttrykket
(Gjør gjerne den samme utledningen, og sjekk om du får samme resultat.)
Dette uttrykket kan forenkles enda mer ved å bruke identiteten
Vi får da at
Når n blir stor, hva vil A nærme seg?
Å beregne arealet A på denne måten, er ganske arbeidskrevende. Vi vil gjerne finne en raskere måte å komme fram til resultatene på. Metoden finnes, og det er dette som er integrasjon. Det arbeidet vi har gjort nå, er på ingen måte nytteløst. Det er slike betraktninger som ligger til grunn for all integrasjonsregning.


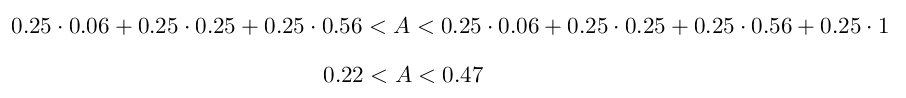

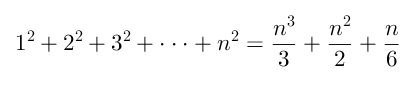

Ingen kommentarer:
Legg inn en kommentar