R1-Størrelse. Komponenter. Skalarprodukt

Vi har allerede lært at en vektor har to egenskaper, størrelse(lengde) og retning. I denne videoen viser vi hvordan vi kan finne lengden av en vektor. Som du vil se, er det Pytagoras setning vi bruker til dette. Vi lærer også hvordan enhver vektor kan uttrykkes som en sum av to ikke-parallelle vektorer.

Til nå vi har lært at vektorer kan summeres og multipliseres med en skalar. Dette kan så igjen gi oss muligheten til å finne differansen av to vektorer. Nå skal vi lære at vi også kan multiplisere to vektorer. Det vi vår ut av denne multiplikasjonen er en skalar, og derfor kaller vi det skalarprodukt.

Videoen som tilhører dette emnet finner du om du går inn her. Notatene som jeg har brukt, kan se på om du åpner denne linken. Også her gis det oppgaver under videoen.

Lykke til !

TN

R1-Parallelle vektorer. Basisvektorer

Vi skal nå arbeide med begrepene parallelle vektorer og basisvektorer. Her handler det først om å lære seg noen definisjoner. Så må du bruke disse definisjonene i problemene som du skal løse.

Som du vil se av videoene, legger jeg opp til mye bruk av rutepapir, linjal og blyant. Du vil ha mye igjen for  gjøre det samme.

Du finner videoen hvis de går inn her. Notatene som jeg brukte, finner du om du åpner denne linken.

Du får noen oppgaver i videoen som du må løse.

Lykke til!

TN

R1-Innledning vektorregning

Vi starter nå med noe helt nytt. Du lærte for lenge siden å telle. Du lærte da å kjenne de naturlige tallene, og det var nok den første matematikken du lærte. Til nå har det meste av matematikken du har arbeidet med handlet om tall. Nå skal du lære om noe helt nytt: Vektorer. Fra nå av skiller vi mellom skalarer, som er de gamle tallene og vektorer, som er det nye vi skal lære om.

Linken til denne videoen finner her. Notatene som jeg har brukt kan du finne om du åpner denne linken.

Videoen inneholder oppgaver som du må løse til neste time.

Lykke til!

1T-LIneær regresjon

Modellering handler om å finne et matematisk uttrykk som kan beskrive et fenomen i naturen eller dagliglivet. Et slikt uttrykk kaller vi en modell. Det finnes en mengde matematiske modeller, og du vil møte dem i mange sammenhenger. I fysikk, kjemi og biologi finnes mange slike modeller.

Lineære modeller er de enkleste modellene. For å finne disse modellene bruker vi noe som heter lineær regresjon. Vi kan regne slike modeller ut for hånd, men oftest tar vi PCen til hjelp for å finne disse modellene. Det trenges mye øving før en behersker dette på en tilfredsstillende måte.

Vidoene tilknyttet dette emnet finner du om går inn link 1 og link 2. Det er ikke tjenlig å se begge videoene rett etter hverandre. Jeg anbefaler at du først video 1 først og prøver å løse noen oppgaver før du begynner på vidoe 2.

Lykke til!

1T-Ettpunktsformelen

Ettpunktsformelen vil du få ofte bruk, ikke bare i år, men i alle årene du er elev her hos oss såfremt du har tenkt å ha matematikk alle tre årene.

Når du vet at en linje går gjennom ett bestemt punkt, og du samtidig kjenner  stigningstallet til  linja, kan du vet å bruke ettpunktsformelen for raskt skrive opp uttrykket for linja.

Videoen for dette emnet finner du om du går inn her.

Etter videoen bør du prøve deg på flere oppgaver. Denne type oppgaver vil du ofte møte.

1T-Grafisk løsning av lineære ligningssett

Vi har gått gjennom løsning av ligningsett ved hjelp av innsettingsmetoden og addisjonsmetoden. Vi har imidlertid flere muligheter;

Med grafisk løsning mener vi at vi tegner ligningene som grafer i et koordinatsystem, og finner løsningene i punktene der  to eller flere kurver skjærer hverandre. Slike grafiske løsninger kan vi gjøre på en vanlig rutepapir, og vi gjøre det ved å tegne kurvene i GeoGebra. Det er viktig å bruke både papir og PC  når du løser oppgavene. Begge deler skal du  beherske.

Vi kan også løse ligningene ved å bruke CAS. I GeoGebra finnes CAS, og dette skal du etterhvert  beherske. Dess tidligere du begynner, dess bedre. I Microsoft mathematics finnes også en ligningsløser som er grei å bruke. Skaff deg erfaring med begge deler.

Videoen til dette emnet finner du her. Det er bra om du, rett etter å ha sett videoen, åpner de samme programmene som jeg har brukt og prøver å gjøre det samme.

1T-Lineære ligningssett

I denne videoen skal vi lære å løse ligningsett med flere ukjente. Vi begynner med to ukjente, men vi skal også lære å løse ligningsett med flere ukjente.

De første ligningsettene vi arbeider med er lineære. Vi skal snakke om hva det betyr når vi møtes i timene. Enkelt kan vi se at det betyr at x og y bare er multiplisert med et tall. Noen ligningsett er ikke-lineære. De skal vi også lære å løse.

Vi lærer to forskjellige metoder for slik ligningsløsning: Addisjonsmetoden og innsettingsmetoden. Du bør beherske begge metodene. Det kan du spare tid på. Noen ligninger lar seg raskere løse med ene metoden. Ofte er det slik at addisjonsmetoden går raskest når den fungerer. Innsettingsmetoden fungerer imidlertid i flere sammenhenger og er derfor mer generell.

Videoen finner du om du går inn  her.

Jeg har ganske sikker på at du vil trenge regnetrening. Det er bare en måte å løse dette på, og det er å løse oppgaver.

Lykke til!

1T-Formelen for stigningstallet

I dette oppslaget konsentrer vi oss særlig om stigningstallet. Dette stoffet pleier ikke å oppleves så vanskelig, og mange elever trener altfor lite på det. Når de så kommer til en oppgave der de trenger å finne stigningstallet for en linje, har de glemt hvordan de gjør det. Sørg for at dette ikke hender deg.

Videoen til dette emnet finner her.

Etter at du har sett videoen, er det oppgaveløsning som gjelder. Løs heller for mange enn for få oppgaver.

1T-Lineære funksjoner

Lineære funksjoner er de første funksjonene vi skal arbeide med. De er enkle å forholde seg til. Prøver vi å tegne dem i koordinatsystem, gir de oss en rett linje. Da du gikk på ungdomsskolen lærte du å kjenne flere av disse funksjonene.

Jeg bruker å si at lineære funksjoner har to hemmeligheter: Stigningstall og konstantledd. I løpet av dette oppslaget skal du lære hva stigningstallet forteller oss og hva konstantleddet forteller oss. Begge er viktige å kjenne til, men det er stigningstallet som vi oftest vil få bruk for.

Når du har lært og forstått de lineære funksjonene, er det kommet et langt stykke videre i din matematiske utvikling fordi kunnskapen om disse funksjonene bruker vi til å lære om alle de andre funksjonene. Derfor vil du ha mye igjen for å få kontroll over de lineære funksjonene.

Du finner videoen til dette emnet her.

Det er flere typer problemstillinger du skal beherske:

1. Du skal kunne lage en tabell med lineære funksjoner
2. Du skal kunne tegne en lineær funksjon i et koordinatsystem
3. Når du ser grafen til en lineær funksjon, skal du kunne finne funksjonsuttrykket. 

Alt dette kan du bare lære ved å løse oppgaver. Det bør du gjøre nå.

1T-Funksjonsbegrepet

Vi begynner nå på et nytt kapittel. Hovedtemaet er lineære funksjoner, men først av alt skal vi prøve å forstå hva en funksjon er for noe. I det første oppslaget er det dette som er temaet.

Du finner videoen til dette emnet her. Det er viktig at du studerer denne videoen nøye fordi her jeg en ganske annen framstilling til funksjoner enn du finner i læreboka.

Når du har sett videoen, bør du som vanlig løse noen oppgaver på egenhånd. Det kan være tjenlig at du holder på inntil du synes det er vanskelig og trenger hjelp

Lykke til

R1-Direkte bevis

Vi skal lære flere bevisformer. Den første heter direkte bevis. Det går i hovedsak ut på at vi begynner med noe som vi vet er sant og så, ved hjelp logikk, utleder noe som vi så også vet er sant. Hovedredskapet  vi under beviset er implikasjonspilen. Den kan vi bruke flere ganger.

Du finner videoen til dette emnet om du går inn her.

Å lære seg  bevisføring er noe som mange elever opplever som vanskelig. Derfor må du regne med at det blir litt prøving og feiling. Det er imidlertid ikke noe alternativ. Det vil ikke finnes noen fasit som i matematikken du har vært vant med til nå. Noen ganger kreves det stor kreativitet for å finne løsninger. Her er det viktig å skaffe seg erfaring

R1-Irrasjonale ligninger

Irrasjonale ligninger er spesielle. Vi kan løse alt helt riktig, men likevel er svaret vi får feil. Dette må vi ta hensyn til hver gang vi har med en slik ligning å gjøre. Hver gang vi har løst en slik ligning, må vi sette prøve på svaret/svarene. Hvis vi ikke gjør det, gjør vi en ikke ubetydelig feil selv om det skulle vise seg at svaret vi har funnet er helt riktig.

Du finner videoen tilknyttet dette emnet om du går inn her. Videoen ble laget til et annet lærebokutgave, så derfor har oppslaget et annet nummer.

Som alltid er det ikke nok å se videoen. Du bør også prøve deg på noen oppgaver før du kommer på skolen.

Lykke til!

R1-Innledning Bevis og bevisføring

Bevis og bevisføring er noe av kjernevirksomheten for en matematiker. Skal en forstå faget og ha framgang, må en derfor vie dette stor oppmerksomhet. I vår gjennomgang vil vi se de to første oppslagene i læreboka i sammenheng. 

Du finner de to aktuelle videoen om du går inn på her og  her. Disse videoene ble laget til en eldre bok, men lærestoffet er det samme. 

Så er det bare å gå i gang med oppgaveløsning. 

1T-Lineært forholdstall

Lineært forholdstall henger nøye sammen med det stoffet vi arbeidet med i de to forrige oppslagene. Vi kan enkelt si at det lineære forholdstallet er en vekstfaktor.

Har vi to likeformede trekanter, vil det være et lineært forholdstall f mellom disse to trekantene. La oss si at det lineære forholdstallet f=3. Er en side i den ene trekanten 2 cm, vil den tilsvarende siden i den andre trekanten være 6 cm.

Eksempel på lineært forholdstall har vi når vi bruker kart. Vi får da oppgitt en målestokk, for eksempel 1:1000. Det betyr at 1 cm på kartet tilsvarer 1000 cm, altså 10 m i terrenget. Her er 1000 det lineære forholdstallet.

Kjenner vi det linenære forholdstallet mellom to trekanter, kan vi også si noe om forholdet mellom arealene trekantene. I eksemplet ovenfor er den andre trekanten 9 ganger så stor som den første. Årsaken er at vi da må multiplisere med kvadratet av det lineære forholdstallet, altså 3∙3=9. Du bør forstå hvorfor det må være slik.

Videoen til dette oppslaget finner du her.

Igjen bør du som vanlig prøve deg på noen oppgaver. Det er det beste måten å sjekke ut om du har forstått stoffet.

Lykke til !

1T-Vekstfaktor

Vi lærer i dette oppslaget en mer effektiv måte å arbeide med prosent på. En del type oppgaver som tar lang tid når vi bruker tradisjonell prosentregning, kan nå løses raskt. Dette stoffet er noe av det du vil få mye bruk for i dagliglivet.

Når du skal finne vekstfaktor, må du stille deg spørsmålet. Er dette prosentvis vekst eller prosentvis nedgang. Er det prosentvis vekst, vil vekstfaktor bli et tall større enn 1. Er det prosentvis nedgang, vil vekstfaktoren bli et tall mellom 0 og 1.

Når du bruker vekstfaktor kan du enkelt både regne deg fram i tid og tilbake i tid. Det går oftest bra når en regner seg fram i tid, men en god del får problemer når de regne seg tilbake. Dette bør de være spesielt oppmerksom på.

Videoen til dette oppslaget finner du her.

Som vanlig bør du nå prøve deg på noen oppgaver.

Lykke til!

1T-Formlike figurer

Formlikhet er et annet av temaene i matematikk som du ofte vil få bruk for. Vi vil særlig arbeide med formlike trekanter. Hvis vi vet at to trekanter er formlike, kan vi bruke opplysninger i den ene trekanten til å finne ut noe om den andre.

Du finner videoen til dette emnet her.

Etter å ha sett videoen bør i gang med oppgaveløsning. Det kreves mye trening for å beherske dette stoffet. Du kan ikke arbeide for mye med dette.

Lykke til

1t-Areal og omkrets

Fra grunnskolen kjenner du flere forskjellige geometriske figurer: Kvadrat, rektangel, trekant, rettvinklet trekant, likesidet trekant, likebeint trekant, parallellogram, rombe og trapes.

Omkrets og areal er to størrelser som vi ofte blir utfordret til å finne. I løpet av årene her vil du møte mange oppgaver som spør om akkurat dette.

Før du går i gang med dette stoffet, er det fint om du tenker over forskjellen på lengde og areal. Gi eksempler på enheter som brukes når vi måler lengder. Gjør det samme med areal.

Videoen knyttet til dette emnet finner du her.

Etter at du har sett videoen bør du regne oppgaver.

R1-Pascals trekant

Pascals trekant er nyttig i flere sammenhenger. Vi møter den i dette kapitlet om sannsynlighet og kombinatorikk, men den har også stor anvendelse når vi arbeidet med algebraproblemer. Å kunne bruke Pascals trekant kan da spare oss for mye regnearbeid.

Du finner videoen til dette emner her.

Som vanlig er det smart å prøve seg på noen oppgaver med en gang. Når du arbeider med Pascals trekant, er den største utfordringen å få riktig fortegn.

Lykke til!

1T-Pytagoras setning

En gang på ungdomsskolen fikk du for første gang høre om Pytagoras setning. Dette er en av de viktigste setningene i matematikken, og den har en rekke anvendelser. Denne setning var viktig på ungdomsskolen, men den blir nok enda viktigere her hos oss.

Pytagoras setning er knyttet til rettvinklede trekanter. Før du går i gang med Pytagoras setning, er det tjenlig å repetere navnene på sidene i et rettvinklet trekant. Tegn derfor en rettvinklet trekant, og sett navn på sidene. Hvilken side er hypotenus og katet?

Nå er det på tid å se videon som du finner ved å åpne denne linken.

I matematikk må føre bevis for de setningene vi bruker. Pytagoras setning må også bevises. I videoen som du finner  her, kan du studere et bevis av setningen

I denne videoen viser jeg et bevis av Pytagoras setning. Det finnes omkring 200 forskjellige bevis av denne setningen, og dette beviset så jeg første gang da jeg gikk på ungdomskolen. Et setning som er bevist, vet vi alltid er sann.

Når du er ferdig med videoen, bør du som vanlig regne oppgaver.

Lykke til !

1T- Dekadiske målenheter. Nøyaktighet

Deka representerer tallet 10. Dekadiske enheter handler om enheter som gjør bruk av tallet 10, enten ved å multiplisere med 10 eller ved å dele på 10.

Et eksempel på en dekadisk enhet er kg. Her betyr k tusen, altså 10∙10∙10. En annen dekadisk enhet er ml som betyr 1l delt på 100. Når du er ferdig å arbeide med dette oppslaget, bør ha lært hva bokstavene G, M, k, h, da, d, c,   m  og μ når de er brukt i dekadiske enheter.

Eksempel på en ikke-dekadisk enhet er måter måler tid på. Vi bruker sekunder (s), minutter (min) og timer (t). Hvilken tall blir brukt her istedenfor 10?

Nøyaktighet er også et tema du får lære om. En hovedregel er at svaret i en oppgave aldri kan være mer nøyaktig enn tallene det bygger på. Det er bakgrunnen for sifferregelen som du finner på side 25.

Du finner videoen til dette emnet om du går inn på denne linken.

Så er det bare å løse så mye mange oppgaver som mulig.

Lykke til!

1T-Kvadratrøtter

Kvadratrøtter har du regnet med da du gikk på ungdomsskolen, men nå skal vi gå enda dypere inn i dette emnet. På mange måter kan vi si at dette blir som å komme inn i en ny og fremmedartet verden. Vi trenger derfor å være der en stund før vi begynner å føle oss hjemme. Du har nettopp startet på en ny skole, og det er mye ukjent i starten. Slik er det også når du begynner å arbeide med kvadratrøtter.

Når vi arbeider med kvadratrøtter, vil du raskt erfare at du får bruk for kvadrattallene. Kvadrattall er et tall du får når du multipliserer et heltall med seg selv. De 11 første kvadrattallene er 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100. Hvordan har jeg kommet fram til disse tallene?

Videoen til dette emnet finner du om du går inn på linken her.

Du husker sikkert hva et kvadrat var for noe. Tegn et kvadrat, og tenk over hvordan du kan illustrere kvadratroten.

Nå er det bare å begynne å løse oppgaver. Det du ikke får til, arbeider vi videre med på skolen i neste time.

Lykke til!

1T-Ligninger

Noe av det du kommer til å bruke mest tid på i matematikk i år, er å løse ligninger. Vi skal lære å løse flere typer ligninger, men felles for alle ligninger er at de kan sammenlignes med en gammeldags skålvekt:

Alle ligninger har et likhetstegn. En ligning balanserer på likhetstegnet på samme med  som en skålvekt. Når vi løser ligninger må vi alltid sørge for at vi gjør det samme på begge sider av ligningen. Det er slik vi løser ligninger.

Du finner videoen til dette emnet her.

Etter å ha sett videoen, bør du løse ligninger. Som i det meste vi gjør, er det øving som gjør underverker.

1T-Grunnleggende algebra

Vi arbeider i matematikk på forskjellige måter. Å telle er eksempelvis den første matematikken du lærer og i løpet av dine første leveår lærer du de første tallene. Vi har allerede vært igjennom hvordan de fire regningsartene kan brukes til å arbeide med tall. Da dine oldeforeldre gikk på skolen, lærte de regning og det var nettopp å bruke de fire regningsartene. Matematikk var er ukjent begrep for de fleste.

 I algebra lærer hvordan vi kan bruke symboler istedenfor tall og sammen med tall. Ved å innføre et symbol som for eksempel x,  kan vi behandle det som et vanlig tall, men det kan representere mange forskjellige tall samtidig. Dette er det viktig at du forstår. 

Det er mye å holde orden på, og da trenger vi arbeide systematisk.  Det blir mindre å passe på, hvis du fører stykkene på en oversiktlig måte. Parenteser av ulike typer bruker vi for å holde orden.

Går du inn på linken her, finner du videoen for dette emnet. Etterpå bør du i gang med oppgaver så raskt som mulig. 

1T-Regning med brøk

Å regne med brøk har du gjort helt siden du gikk på barneskolen. Her hos oss vil du også få bruk for brøkregning. Det er derfor viktig at du nå tar deg tiden du trenger for å bli trygg i brøkregning.

Vi snakker ofte om de fire regningsartene addisjon, subtraksjon, multiplikasjon og divisjon. Du trenger å kunne addere og subtrahere brøker, og du trenger å kunne multiplisere og dividere brøker. Det kan være tjenlig å systematisere arbeidet med brøk slik:

Det å  addere eller subtrahere to brøker, er ofte det som er vanskeligst. Et nøkkelbegrep i denne sammenhengen er fellesnevner. For å kunne addere eller subtrahere to brøker, må de ha fellesnevner. Å multiplisere og dividere brøker er mye lettere. Her er det ikke å tenke på fellesnevner.

Når du nå bør se videoen om emnet, er det bra om du reflekterer over dette. Du finner videoen her.

Du trenger øving for å lære dette skikkelig, så det er bare å sette i gang med å løse oppgaver. Etterhvert bør du løse oppgaver uten å se i læreboka.  

R1-Binomisk sannsynlighetsfordeling

Binomiske sannsynlighetsfordeling har mye til felles med hypergeometrisk fordeling, men det er en viktig forskjell:

I eksemplet jeg viste på hypergeometrisk sannsynlighet, handlet det om å trekke fra en hatt med  20 lodd hvor 3 lodd var vinnerlodd. Når du starter er sannsynligheten for å vinner 3/20. Når du først har trukket ett lodd, endrer sannsynligheten seg for å trekke et vinnerlodd, uansett om du har trukket et vinnerlodd eller ikke-vinnerlodd. Årsaken er ganske åpenbar: Når du har trukket ett lodd, er det 19 lodd igjen. Da er sannsynligheten for å vinne enten 2/19 eller 3/19, avhengig om du har første gang har trukket et vinnerlodd eller ikke.


La oss si at vi skal gjennomføre en rekke med n identiske forsøk. Vi kan bruke en binomisk sannsynlighetsmodell hvis følgende tre kriterier alle er oppfylt:

1. Vi kan skille mellom to ulike utfall, suksess og fiasko.
2. Sannsynligheten for suksess er like stor ved hvert forsøk. (Dette gjelder ikke for hypergeometrisk sannsynlighetsfordeling)
3. De ulike forsøkene er uavhengig av hverandre.   

Vi lærer en enkel formel som vi kan bruker for å regne ut binomiske sannsynlighetsfordelinger, se side 29, gul firkant. De fleste lærer raskt å bruke denne formelen.  Derimot er det en større utfordring  å begrunne at vi har en binomisk sannsynlighetsfordeling. Vi skal også lære hvordan vi gjør de samme utregningene i GeoGebra.

Videoen til dette emnet finner du her.

Så gjenstår det å regne oppgaver.

R1-Hypergeometrisk sannsynlighetsfordeling

Hypergeometrisk sannsynlighetsfordeling lar seg enklest forklare ved et eksempel:

Eksempel
La oss si at vi i et hatt har 20 lodd hvor tre av loddene er vinnerlodd. Du skal trekke ut tre lodd. Hva er sannsynligheten for at du vinner på to av loddene?

Dette eksemplet kan løses ved hjelp av hypergeometrisk sannsynlighetsfordeling. Vi kan dele loddene i to atskilte typer, vinnerlodd og ikke-vinnerlodd. Når du har trukket et lodd, blir det ikke lagt tilbake. Hypergoemetrisk og binomisk sannsynlighetsfordeling ligner på hverandre. Det er en vesentlig forskjell mellom dem. Når du har forstått det, har du kommet langt i forståelsen av disse sannsynlighetsfordelingene.

De fleste lærer seg ganske raskt  å bruke formelen for hypergeometrisk fordeling som du finner s. 27, gul firkant. Husk at før du bruker formelen, må du ha begrunnet at vi har en hypergeometrisk fordeling. Vi skal også lære hvordan vi gjør de samme utregningene i GeoGebra.

Du finner videoen til dette  oppslaget om du går inn på linken her.

Når du har sett videoen, bør du prøve deg på oppgaver.

R1-Sannsynlighetsfordelinger

Det finnes mange forskjellige sannsynlighetsfordelinger. Vi skal særlig bli kjent med to slike, hypergeometrisk sannsynlighetsfordeling og binomisk sannsynlighetsfordeling. Vi vil lære om disse fordelingene i de to neste oppslagene, men i dette oppslaget skal vi lære hva som er felles for alle sannsynlighetsfordelinger.

I alle sannsynlighetsfordelinger gjelder at summen av alle sannsynlighetene er lik 1. Dermed har vi en enkel metode for å sjekke om vi  har en sannsynlighetsfordeling

Videoen tilknyttet dette emnet finner du her.

Etter å ha sett videoen, bør du som vanlig prøve deg på noen oppgaver.

R1-Bayes' setning

Bayes' setning er en setning som vi får bruk for i en del sammenhenger når vi arbeider med betinget sannsynlighet. Du bør både merke deg hvordan du utleder setningen, se øverst på side 23.

Videoen tilknyttet dette emnet finner du om du går inn på linken her.

Etter å ha sett videoen bør du regne noen oppgaver. Lykke til

R1-Produktsetningen

Dette oppslaget er også repetisjon av stoff vi gikk igjennom i fjor.

1. Husker du definisjonen av disjunkte hendinger?
2. Husker du definisjonen av uavhengige hendinger?

Så møter vi igjen produktsetningen. Her må vi merke oss at det finnes to utgaver av denne setningen.

1. Produktsetningen for uavhengige hendinger.
2. Produktsetningen for avhengige hendinger.

I tillegg får vi et gjensyn med addisjonssetningen for disjunkte hendinger.

Ved  å gå inn på denne linken, finner du en video som omhandler dette oppslaget. Hvis du ønsker å se de videoene vi brukte i fjor, kan du gå inn på linkene link2 og link3.

Som vanlig, bør du nå gå igang med oppgaver

Lykke til !

1T-Regnerekkefølge

Et oppgave som 1+2∙3, har flere mulige svar, men bare ett er riktig. For at vi skal finne dette svaret, må vi kjenne til og forstå hva regnerekkefølge betyr. I læreboka angis følgende regnerekkefølge.

Du kan prøve deg selv på noen oppgaver. Hvis det går greit, fortsetter du bare å regne. På et eller annet tidspunkt er det greit om du ser videoen som du finner her. Du vil se at jeg har et litt annen tilnærming til stoffet enn læreboka.

I læreboka er det foreslått at du bruker følgende regnerekkefølge

1. Regn ut potenser
2. Multipliser og divider
3. Regn sammen( Adder, subtraher)

For at du skal forstå hva jeg nå har skrevet, må du kjenne til begrepene potenser, multiplikasjon, divisjon, addisjon og subtraksjon. Husker du hva disse begrepene betyr?

Hva blir svaret på oppgaven ovenfor?

1T-Prosent

Prosentregning har du lært i grunnskolen, og dette oppslaget lærer deg ikke så mye nytt. Det er ikke laget en egen video for dette oppslaget. Vi gjennomgår det meste på skolen.

Legg merke til at vi bruker prosent på forskjellige måter. Du kan få oppgaver som

1. Du tjener kr. 120 i timen og får en lønnsøkning på 10 %. Hva blir den nye lønna?
2. En vare koster kr. 150 etter å ha blitt satt ned med 12 %. Hva var den opprinnelige prisen? 
3. I en klasse på 24 elever er 11 gutter. Hvor mange prosent gutter er det i klassen?

Det er viktig at du raskt lærer deg forskjellene på disse måtene å bruke prosent på. Her gjøres det unødvendig mange feil.

Lykke til!

1T-Veien om 1

Første kapittel i læreboka vår har overskriften "Matematikken rundt oss". I dette kapitlet vil lære om hvordan matematikken kan være til hjelp for oss når vi skal løse ulike typer problemer i hverdagen vår.

I det første oppslaget handler det om å bruke metoden "veien om 1". Vi går igjennom noen eksempler på denne metoden i de to første timene, men går du glipp av dette, er det ingen ulykke. Dette er stoff som du helt sikkert har møtt tidligere. Det går også greit å lese teksten i læreboka. Det viktige er at du kommer i gang med oppgaveløsning.

Hvis det er oppgaver du ikke klarer å løse, er det viktig at du spør om hjelp.

Seinere vil du finne link til en video, men det mangler her. Du vil finne første video når du kommer til oppslag 1.3 Regnerekkefølge.

Lykke til!

R1-Betinget sannsynlighet. Uavhengige hendinger

I dette oppslaget er også mye av stoffet repetisjon fra forrige skoleår. Det å forstå betinget sannsynlighet er noe av det som er mest krevende i dette kapitlet. Om du må streve for å forstå dette, kan du trøste deg med at du ikke er den første.

Det finnes ikke noen enkel måte å lære dette på. Du må først gå i gang med å lære deg definisjonene. I læreboka s. 18 og 19 finner du  gule firkanter som definerer Betinget sannsynlighet og Uavhengige hendinger.

I sannsynlighetsregning fikk vi bruk for den del av matematikken som kalles mengdelære. Her lærte vi også en del nye begreper og ny notasjon. Dette er det greit å repetere nå:

For å forstå og kunne bruke formelen som betinget sannsynlighet:

,

er det nødvendig å ha forstått snitt og union i mengdelæren. 

Dette er altså noen de utfordringene du møter i dette oppslaget, men nå er det sikkert på tide å se videoen som omhandler dette emnet. Du finner den her.

Nå bør du prøve deg selv i å løse oppgaver. Prøv deg på oppgavene 1.24-1.28. Du kan også finne andre oppgaver om du ønsker. 

I neste time vil vi først bruke sette av tid til å løse oppgaver du ikke har fått til. Så blir det avsatt til oppgaveløsning. Mot slutten av timene vil det gjennomføre en test om du behersker dette stoffet. Det gjelder både dette og foregående oppslag. 

Lykke til!

R1-Sannsynlighet ved opptelling

I dette oppslaget går vi igjennom stoff som egentlig er repetisjon. Vi lærte sist år om Uniforme sannsynlighetsmodeller. Det er dette vi går vi videre på i dette oppslaget. Det meste av dette er altså repetisjon.

I en Uniform sannsynlighetsmodell, har alle enkeltutfall like stor sannsynlighet.  Vi lære oss å bruke formelen  for uniform sannsynlighet:

Da blir det ganske enkelt å beregne sannsynlighet. Vi må bare kunne telle gunstige og mulige utfall.

Du finner videoen til dette oppslaget ved å gå inn på linken her.

Gå så i gang med å løse oppgaver 1.24-1.28. Det er viktig at du ikke gir deg så lett. Prøv flere ganger om du får problemer. Du kan også se videoen pånytt, så du er sikker på at du har forstått stoffet.

I  starten av neste time vil regne igjennom eventuelle oppgaver som du og andre ikke har fått til. Det er da viktig at du har prøvd deg skikkelig for å få maksimalt utbytte av denne gjennomgangen.

Lykke til!

R1-Antall kombinasjoner

I dette oppslaget får vi igjen presentert nye begreper. Det nye begrepene er Uordnede utvalg og Antall kombinasjoner. Når noe er ordnet har rekkefølgen betydning. I et uordnet utvalg har rekkefølgen ikke noen betydning:

Hvis du er blant tre som har vunnet et tur til Amerika, har det ingen betydning om du blir trukket ut først eller sist. Uansett kommer du med på turen. Hvis premiene i et lotteri er på kr. 20 000, kr. 10 000 eller kr. 500, har det betydning hvilken premie du vinner.

Begrepet Antall kombinasjoner har en spesiell notasjon som ser slik ut:

Vi kan lese dette på forskjellige måter. I læreboka  foreslår de to måter: "Av n velg r" eller "n over r". Jeg er skeptisk til den siste formuleringen fordi denne kan forveksles med brøk. Brøken fem todeler leser vi som kjent "Fem over to".

I annen litteratur brukes Binominalkoeffisienten på samme måte som Antall kombinasjoner. Når du seinere skal studere matematikk, vil det være denne formuleringen du møter.  En alternativ lesemåte som ikke er til å misforstå, er  Binominalkoeffisienten n over r.

Det er igjen fint om du prøver å få innhold i de nye begrepene før du ser videoen som du finner her.

Gå så igang med å løse oppgavene 1.14-1.18. Hvis dette går greit, kan du også prøve deg på oppgaver som du finner i arbeidsplanen i itslearning.

R1-Antall permutasjoner

Permutasjoner er et nytt begrep som du nå skal lære deg. Begrepet permutasjoner er nært knyttet til et annet nytt begrep: Utvalg uten tilbakelegging.  Det siste nye begrepet Ordnet utvalg. Som du vil se, når du slår opp på sidene 12-13, har alle disse begrepene fått hver sin gule firkant. Dette er et tegn på at disse begrepene bør læres så raskt som mulig.

Det er ikke nok å bare igjenkjenne dem. Du bør arbeide så mye med at de etter hvert begynner å sitte i fingrene. Studer derfor litt nøye disse firkantene før du du ser på videoen som du finner ved å gå inn på linken her. I innledningen i videoen oppdaget jeg en trykkfeil. Denne videoen tilhører selvsagt Matematikk R1.

Etter å ha sett videoen, er det bare å gå i gang med å løse oppgaver. Alle oppgavene 1.7-1.13 er relevante oppgaver som du bør løse før du kommer på skolen. I starten av timene vil jeg åpne for spørsmål, slik at du får hjelp med oppgaver som du ikke har fått til. 

Den testen som jeg forberedte deg på i forrige innlegg, vil også dekke dette oppslaget. Testen vil bli gjennomført på slutten av de to arbeidsøktene vil skal ha på onsdag. 

Hvis du får problemer med noen oppgaver når du sitter hjemme, er det ingen grunn til bekymring. Det du bør gjøre hvis du står fast, er å prøve igjen. Hvis det fortsatt ikke blir riktig, kan du forsøke andre oppgaver. Det kan også være tjenlig å se videoen pånytt. Da kan det hende at du forstår ting som du ikke forsto ved første gangs gjennomgang. 

Når du så kommer på skolen, vil du få hjelp av meg til å løse oppgaven. Det at du har slitt en del med oppgaven på forhånd, vil sikre at du både forstår og husker løsningen til du skal løse en lignende oppgave seinere. 

Lykke til med arbeidet!

R1- Mulitplikasjonsprinsippet. Fakultet

Første kapittel i læreboka vår Sigma R1 har overskriften "kombinatorikk og sannsynlighet". Sannsynlighetsregning har vi arbeidet med før, men kombinatorikk er nytt. men som du vil erfare, er dette bare delvis nytt.

Kombinatorikk handler grovt sett om å telle og å telle på smarte måter. Dette krever en del omtanke, men også mye trening.

I det første oppslaget er overskriften Multiplikasjonsprinsippet. Fakultet. Når du slår opp i læreboka, vil du se at både Multiplikasjonsprinsippet, Utvalg med tilbakelegging og Fakultet har fått hver sin gule firkant. Når du går i gang med arbeidet, kan det være tjenlig å studere teksten i disse firkantene litt og gjøre deg noen tanker om hva de betyr. Dernest bør du se videoen som du finner ved å gå inn på linken her.

Når du har sett videoen, bør du selv gå i gang for å løse oppgaver. Du bør på eksemplene s. 10-11 og oppgavene 1.1-1.5.

I onsdagstimene vil det bli gjennomført en test som viser om du har forstått disse grunnleggende begrepene, men før det vil vi sammen arbeide med oppgaver som dere ikke har fått til hjemme. Det vil også bli satt av tid til å arbeide med oppgaver.

Lykke til!  

1T-Hyperbler. Asymptoter

Vi har tidligere sett en video om kjeglesnitt. De mest kjente kjeglesnittene er ellipsen, parabelen og hyperbelen. Ellipsen lærer vi mer om til neste år. I dette kapitlet har du allerede lært om parabelen. Nå står hyperbelen for tur. Videoen tilknyttet dette emnet finner du om du åpner denne linken.

Når vi arbeidet med hyperbler og rasjonale funksjoner, møter vi raskt begrepet asymptoter. Asymptoter er linjer som er spesielt tilknyttet funksjonen og som derfor kan fortelle oss mye om funksjonene. Det er derfor svært nyttig å finne disse linjene. Vi kan oppleve tre forskjellige typer asymptoter: Vertikale asymptoter, horisontale asymptoter og skråasymptoter. Du lærer i dette oppslaget hvordan vi kan finne både vertikale og horisontale asymptoter.

Det er alltid lurt å starte med de vertikale asymptotene. Da spør du deg: Hvilke verdier av x gjør at nevneren vår blir lik null. Svaret på dette spørsmålet gir oss de vertikale asymptotene. I videoene vil du få forklart hvordan vi finner det horisontale asymptotene. I en time vil jeg vise funksjoner som har skråasymptoter.

Prøv løse oppgave 7.22 på egenhånd først. Når du er ferdig eller ikke får til mer, kan du se på videoen løsningsforslag 7.22.

1T-Rasjonale funksjoner i praktiske situasjoner

Da vi gikk i gjennom ulike tallmengder lærte vi om de naturlige tall N, de hele tall Z, de rasjonale tall Q og de reelle tall R.   Vi husker at rasjonale tall var alle tall som kunne uttrykkes som brøk. De rasjonale funksjonene er alle funksjoner som består av en brøk og der nevneren inneholder x.

Vi har arbeidet mest med  polynomfunksjoner, og da spesielt lineære funksjoner. Det er ikke så mye å passe på når det gjelder slike funksjoner. Når vi nå skal arbeide med rasjonale funksjoner, blir det mer å passe på. Årsaken til dette er at vi ikke kan bruke verdier av x som gir null i nevneren.

Rasjonale funksjoner har også sine anvendelser, og det er slike anvendelser som vi er hovedtemaer i dette oppslaget. Du finner videoen tilknyttet dette emnet om du åpner denne  linken.

I dette oppslaget er det også greit om du bare bruker GeoGebra når du løser oppgavene. Seinere må du trene på å tegne slike funksjoner for hånd. De funksjonene som du møter i dette oppslaget er ikke egnet for slik trening.

1T-Bruksområder for andregradsfunksjoner

De funksjonene som vi arbeider har ulike bruksområder. Andrefunksjonene har mange anvendelser. Eksempelvis vil alle kast følge en andregradsfunksjon hvis vi klarer å minimere eller se bort fra luftmotstanden. Banen til kulene som brukes i kulestøt, friidrett, vil følge en omtrent perfekt andrefunksjon.

Videoen som tilhører dette emnet finner du om du går inn på denne linken. Notatene som jeg brukte da jeg laget denne videoen har jeg ikke lengre, så det må du klare deg uten.

Du skal kunne tegne grafene til funksjonene vi arbeider med både for hånd og ved å bruke GeoGebra. I dette oppslaget er greit å bare bruke GeoGebra. I andre sammenhenger er det viktig at du trener på å tegne funksjonene for hånd.

Sørg for å løse så mange oppgaver som mulig.

1T-Parabler

Parabler er en type kurve som har vært kjent siden antikken. Det hører sammen med noen andre kurver som vi kaller kjeglesnitt. Andre kjeglesnitt er sirkelen, ellipsen og hyperbelen. Det er viktig å kjenne til disse kjeglesnittene, og du vil møte dem i forskjellige sammenhenger. Derfor starter vi med en innledning om kjeglesnitt.

Deretter ser vi nøyere på parabelen. Den kan lære ved å se videoen om parabler. De parablene vi møter i dett kapitlet er enten blide eller sure. Det kan du lære mer om hvis du åpner denne linken.

I de to videoen som nå følger, viser jeg hvordan vi løses to oppgaver, oppgave 7.12 og oppgave 7.13: Oppgave 7.12 og Oppgave 7.13. Du vil trenge læreboka når du ser på disse videoene.

De er nå fint om du selv prøver å løse oppgaver selv. Løs gjerne først de oppgavene du allerede har sett løsningen til.

1T-Definisjonsmengde og verdimengde

Den første videoen som er tilknyttet dette emnet finner du om åpner denne linken.

Dette stoffet oppleves vanskelig for mange elever. Du må derfor regne med at det kreves tid for å forstå det. Se gjerne igjennom videoen flere ganger, og prøv å løse noen av de første oppgavene. Hvis det ikke går, starter du den neste videoen som du finner om du link2.

Jeg har også laget en video som viser hvordan vi kan bruke GeoGebra til å løse oppgave 7.1. Du finner videoen om du åpner linken Oppgave 7.1. Jeg har sett igjennom denne videoen igjen og erkjenner at det nok ikke ville laget den på samme måte i dag.  Det som imidlertid er bra, er at du får god innsikt i noen nyttige kommandoer i   GeoGebra. Jeg anbefaler deg derfor å bruke den tiden det tar å se videoen, og så prøve om du får til det samme selv.

Når du er ferdig med dette, er det bra om du prøver deg på noen oppgaver.

Lykke til

1T- Løsning av ulikheter ved hjelp av fortegnslinjer

Det er to videoer tilknyttet dette emnet. Den første videoen finner du her. Når du har sett videoen er det lurt å løse noen oppgaver som er de samme eller lignende ulikheter som du så løsningen av i videoen.  Den neste videoen finner du  om du går på del 2. Prøv å løse enda flere oppgaver etter å ha sett denne videoen.

I høst arbeidet vi mye med multiplikasjon av tall med ulikt fortegn. Vi husker at produktet av to positive tall er positivt, produktet av et negativt og positivt( og omvendt) er negativt og produktet av to negative tall er positivt. Vi kan formulere dette slik: Produktet av tall med ulike fortegn blir negativt. Produktet av like fortegn blir positivt. Dette blir svært viktig å huske i arbeidet med ulikheter. 

1T-Lineære ulikheter. Fortegnslinjer

Vi starter nå et nytt kapittel som har fått navnet Grafer og ulikheter. Vi går da et stykke videre i forhold til det vi lærte i algebra tidligere i år. Vi har allerede lært å løse forskjellige ligninger, men nå møter vi ulikhetene. Vi kan behandle ulikhetene som vi behandler ligninger, men det er noen viktige forskjeller. Er vi ikke oppmerksomme på disse forskjellene, kan løsningene våre bli uriktige.

Det er ialt 4 videoer knyttet til dette emnet. Jeg gjør oppmerksom på at dette var de første videoen for undervisningsbruk som jeg laget. I dag lager jeg videoer på en annen måte. Matematikken som vi går igjennom, kan du likevel stole du. De to første videoene bør du se i rekkefølge. Her går vi går vi blant annet igjennom de forskjellige ulikhetstegnene. Det er viktig at du forstår forskjellene mellom likhetstegnet og ulikhetstegnene. Du finner videoene ved å gå inn på video 1 og video 2.

Når du har sett disse videoen, skal vi lære hvordan vi løses enkle lineære ulikheter. Videoen tilknyttet dette emnet finner du her. Det er sikkert lurt å prøve å løse noen slike ligninger rett etter at du har sett videoen. Både oppgave 7.1 og 7.30 er her alternativer.

Et viktig redskap når vi arbeider med ulikheter, er fortegnslinjer. Videon tilknyttet dette emnet finner du her . Prøv også å tegne noen fortegnslinjer når du har sett videoen. Se oppgaver på arbeidsplanen.

Hvis du har fått gjort alt dette til neste time, kan du være godt fornøyd med arbeidsinnsatsen.

1T- En oppgave. To løsninger

Videoen tilknyttet dette temaet finner du her. Du finner notatene om du åpner linken notater.

Dette innlegget er ikke ferdig ennå, men linkene ovenfor kan brukes. Lykke til !

1T-Bevis tre setninger i trigonometri

Videoen som er tilknyttet dette emnet finner du ved å gå her. Notatene som jeg har brukt, kan du studere om du går inn på notater.

Først i denne videoen gikk vi i gjennom tre definisjoner: Supplementvinkler, komplementvinkler og motsatte (omvendte ) vinkler. Du fikk også noen oppgaver å løse tilknyttet disse definisjonene. Bakgrunnen for dette er todelt.

1. Det å arbeide med definisjonene gjør at vi lettere lærer definisjonen. Definisjoner må bare læres. De er som gloser når du lærer engelsk. Det blir helt håpløst å snakke engelsk hvis du ikke kan noen engelske ord. 
2. Du skal forstå og lære setningene som er tilknyttet hver av disse definisjonene. 

Dette vil du få bruk for i mange sammenhenger, så dess raskere du lærer deg disse definisjonene med medfølgende setninger, dess lettere blir det løse oppgaver. Vi får egentlig ikke brukt disse setningene når vi beviser setningene, men i stoffet som kommer i neste video, blir dette høyst aktuelt.

Bevisene er av forskjellig vanskelighetsgrad. Jeg gjennomfører bevisene slik at vi gjør det enkleste først. Å bevise cosinussetningen er nok det vanskeligste. Du må ikke regne med at du skal forstå alle bevisene med en gang. Derfor bør du studere dem flere ganger, både med video og uten video.

1T-Areal-, sinus- og cosinussetingen

Videoen tilknyttet denne videoen finner du ved å gå inn på denne linken. Notatene som jeg brukte under produksjonen kan du studere om du åpner notater. Du bør se videoen og studere notatene før du går videre på teksten under.

Dette kapitlet dreier seg egentlig om disse tre setningene. I videoen har jeg vist noen av de anvendelse som disse setningene har. I de eksemplene som jeg viste, kunne vi bruke setningene uten å tenke oss så mye om. Merk deg følgende om disse oppgavene:

1. Alle vinklene var spisse, altså mellom 0° og 90°. Blant annet kunne vi se det greit fra figurene fordi forholdene mellom alle sidene var tegnet nøyaktig. Det kan bli annerledes hvis én vinkel er stump, altså mellom 90° og 180°. 
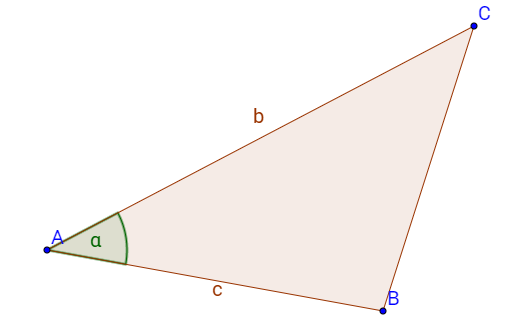
2. Hvis vi en trekant har fått oppgitt lengden av to av sidene og den mellomliggende vinkelen mellom disse sidene, er vi helt trygge. Se trekanten under:

I denne trekanten  kjenner vi sidene AB og AC. De har henholdsvis lengden c og b. Den  mellomliggende vinkelen til sidene AC og AB, er vinkelen som vi markert. I en slik situasjon er alt bestemt. Vi kan både bruke arealsetningen, sinussetningen og cosinussetningen med vellykket resultat. Det blir helt annerledes om vi fikk oppgitt de samme sidene, men én av de andre vinklene. 

Noen ganger kan en oppgavebeskrivelse gi to løsninger. Det skal vi nærmere på i videoen "En oppgave. To løsninger". Det gjelder å kjenne igjen situasjoner når vi er helt trygg, og situasjoner der vi kan få flere løsninger.

1T-Enhetssirkelen

Videoen som er tilknyttet dette emnet finner du ved å gå inn her

Notatene som jeg har brukt da jeg lagde videoen finner du ved å gå inn på notater.

Her finner du linken til geogebra-filen med enhetssirkelen: Enhetssirkelen. Bruk enhetssirkelen til å finne sinus og cosinus til følgende vinkler: 0°, 50°, 80°, 115°, 155°, 220°, 330°.

Hvis du har skjønt hvordan enhetssirkelen fungerer, vil du klare å fylle ut skjemaet som du finner ved å gå inn her. Dette er stoff som du bør beherske og som du derfor vil bli testet om du kan. 

I videoen har vi i realiteten løst oppgave 6.3 og 6.4. Du vil ha løst oppgave 6.13 når du fylt ut skjemaet ovenfor. 

Du skulle nå være rustet til å gå i gang med alle oppgaver som du finner i oppslagene 6.1- 6.4. Løs oppgavene 6.1-6.19 først.

Lykke til!

1T- Innledning om trigonometri

Endelig har jeg fått komme i gang igjen og produsere nye undervisningsvideoer. Videoen til dette emnet finner du om du går inn på linken her. Notatene som jeg brukte da jeg lagde videoen finner du om du går inn på notater. Du bør se videoen, før du går videre i denne teksten.

Som du har sett, startet vi med å oppsummere hva vi vet om trekanter fra før. Det meste av det du kan om trekanter, lærte du i grunnskolen, men noe har du nok lært i løpet av dette første året i videregående skole. Ikke minst har vi brukt tid på repetere stoff som du har vært borti før. Derfor er nok forståelsen din for stoffet betydelig høyere enn det den var da du startet her hos oss.

Det er som regel klokt å gjøre slike oppsummeringer før en starter med nytt stoff. Det bør du derfor selv gjøre til en vane.

Trigonometrien hviler på tre definisjoner:

Vi setter ofte opp ligninger når vi skal løse den type oppgaver som vi møter i dette videoen. Det må du også gjøre når du kommer til oppgavene i læreboka. Da gjelder det at du løser disse ligningene riktig. Husk da på skålvekta som vi har tatt fram i mange sammenhenger. 

Lykke til !

1T-Kvadratsetningene

Videoen tilknyttet denne teksten finner du ved å gå inn her. Du bør se videoen før du  leser videre på denne teksten. Notatene som jeg brukte i videoen finner du ved å gå inn på på notater.

Som du kan observere, begynner vi dette kapitlet på en litt uvanlig måte. Vi starter ikke med oppslag 5.1 Tallmengder, Intervaller som en kanskje kunne forvente. Derimot går vi rett på en svært praktisk oppgave. Det er en fordel om du har sett videoen og forberedt deg litt før du kommer på skolen. I timen vil dere få utlevert papir og sakser. Skrivesaker regner jeg med at dere har selv.

Resten blir problemløsning, og dere må regne med at ikke alt er like enkelt. Husk at dette skal løses praktisk. Det er ved å klippe eller brette, at dere kommer fram til løsningene.

R2-Integrasjonsteknikker

Videoen som er tilknyttet denne teksten, finner du om du går inn her.
Notatene som jeg brukte i videoen finner du om du åpner notater.
Denne teksten er ikke ferdig, men publiseres slik at du kan nå disse to linkene.

TScB-Vurdering av en sykdomstest

1T-Union. Addisjonssetningen

Videoen tilknyttet dette innlegget finner du her. Du finner notatene som er brukt i videoen om du åpner notater.

Denne teksten er ikke ferdig, men er åpnet slik at du skal ha tilgang til linkene.

1T-Disjunkte hendinger. Total sannsynlighet

Videoen tilknyttet dette innlegget finner du her. Du bør se videoen for å ha fullt utbytte av denne teksten. Notatene som jeg bruker i videoen finner du når du åpner notater.

Denne teksten er ikke ferdig, men er likevel åpnet fordi den gir linkene som du trenger for å arbeide med stoffet

1T-Venndiagram

Videoen tilknyttet dette innlegget finner du her. Du bør se videoen for å ha fullt utbytte av denne teksten. Notatene som jeg brukte i videoen, finner du om du åpner linken notater.

Venndiagram er et svært nyttig redskap for å løse flere typer problemstillinger innenfor sannsynlighetsregning. Jeg vurderer det ikke som spesielt vanskelig. Jeg har erfart at alle elever som legger inn en skikkelig innsats, lykkes med å beherske dette stoffet.

Det trenges trening for å bli flink til å sette opp slike diagrammer, så her er det ikke nok å se på at andre løser slike oppgaver. Du må gå i gang selv. Det er viktig å trene både med og uten bok. Det er helt sikkert at du vil møte slike oppgaver en rekke ganger. Dess mer du har trent, dess større er muligheten for å lykkes.

TScB-Fødseldagsproblemet

1T-Komplement. Sannsynligheten for minst én

Videoen tilknyttet dette innlegget finner du her. Du bør se videoen for å ha fullt utbytte av denne teksten.
Notatene som jeg brukte i videoen finner du om du åpner linken notater.

Når en har skjønt det stoffet som vi går igjennom i denne videoen, har en kommet langt. Ikke alt dette er så lett tilgjengelig, og du må regne med å bruke noe tid.

Jeg stiller i alt tre spørsmål i videoen som du utfordres til å finne svar på. De refereres muntlig i videoen, men går du inn i notatene, finner du også spørsmålene der. De to første skulle ikke være så vanskelige, men fødselsdagsproblemet er en utfordring. Her finner du en link til fødselsdagsproblemet: Fødselsdagsproblemet

De to første spørsmålene, vil vi snakke om i førstkommende time. Det finnes mange grader av svar. Det mest grunnleggende er at en kan referere spørsmålet.

Lykke til!

R2-Regneregler for integrasjon. Areal mellom grafer. Samlet mengde

Videoen tilknyttet denne overskriften finner du her. Du bør se videoen for å få fullt utbytte av denne teksten.


Det er tre setninger tilknyttet funksjonene f(x) og F(x), og g(x) og G(x)  som står sentralt i denne videoen. Det er følgende sammenheng mellom disse funksjonene:

     

Da gjelder følgende regneregler:

Det er en fjerde setning, som vi allerede har brukt, og som vi vil komme tilbake til igjen og igjen. Denne bør du også lære deg og forstå. Det er:

Du kan sjekke ut denne setningen ved å se på følgende eksempel:

1T-Snitt mellom hendinger. Produktsetningen

Videoen tilknyttet denne overskriften finner du på her. Du bør se videoen for å ha utbytte av denne teksten.

I forrige oppslag arbeidet vi betingede sannsynligheter og uavhengige/avhengige hendinger. Dette stoffet får du  bruk for her. Hvordan avgjør vi om to hendinger er uavhengige? Spørsmålet har et helt presist svar som vi nå kan repetere:

I videoen får du en del oppgaver som du skal arbeide med. Du finner dokumentet som jeg brukte og opgavene om du går inn på denne linken. 

Mine løsninger på oppgaven finner du her, men denne siden åpner jeg ikke ikke før etter at dere har arbeidet en stund med oppgavene. 

Lykke til med oppgaveløsningen

R2-Mer om integraler og arealer

Videoen tilknyttet til dette innlegget finner du her. Du bør se videoen for å ha fullt utbytte av denne teksten.

Da vi innledet dette kapitlet, studerte vi sammenhengen mellom integraler og arealer. Ofte kan vi sette likhetstegn mellom integraler og arealer, men ikke alltid. Måler vi et areal, er størrelsen alltid større eller lik null. Integraler kan kan derimot både være positiv, negative og lik null. Det avgjørende er om grafen til kurven er over eller under x-aksen slik vi ser i denne videoen.

Når vi skal beregne arealer mellom grafen og x-aksen, må vi derfor ta hensyn  til om grafen ligger over og under x-aksen. Eksemplet med sin(x) viser dette med all tydelighet. Når vi får oppgave der vi skal beregne arealer mellom en grafen og x-aksen, vil det ofte være tjenlig å finne nullpunktene til funksjonen.

De integralene som vi skal løse i dette oppslaget, kan vi løse raskt hvis vi kjenner de antideriverte til de grunnleggende funksjonene. Jeg tenker da særlig på funksjonene som du finner på denne listen:

 På det nivået som vi er, er det å kunne dette listen den viktigste forutsetningen for å få suksess. Mer avansert intervallregning blir ytterst vanskelig hvis ikke disse antideriverte er i korttidsminnet.

1T-Betinget sannsynlighet. Uavhengige og avhengige hendinger.

La A og B være to hendinger.
P(A|B) betyr at det er lagt inn en betingelse for at A skal være oppfylt. B er betingelsen. P(A|B) er altså den betingede betingelse for at A er oppfylt.

Jeg har erfaring med at dette stoffet fortoner seg vanskelig for mange elever. Vanskelighetene blir betydelig mindre hvis en lærer seg å spørre. Hva er betingelsen?

Tabellen over viser den ferdig utfylte krysstabellen i oppgave 4.15. Det viste seg å være lurt å fylle den ut. Generelt gjelder at krysstabeller er et egnet redskap når vi arbeider med betingede sannsynligheter.

P(S|G) leser vi "P av S gitt B". Her er G betingelsen. Vi skal altså finne ut hva sannsynligheten er for at en gutt har mp3-spiller.

Vi har en intuitiv, språklig forståelse av hva det betyr om to hendinger er avhengige av hverandre eller uavhengige. I matematikk er ikke dette tilstrekkelig. Vi trenger en mer presis definisjon. Hvis vi skal avgjøre om S og G er uavhengige, må følgende spørsmål besvares:

Er P(S)=P(S|G)? 

Er svaret Ja, er hendelsene uavhengige. Er svaret nei, er det avhengige.

Her nytter det altså ikke med synsing. I svaret på et enkelt spørsmål, finner vi løsningen.

1T- Store talls lov

Store talls lov 

"Når vi gjentar et forsøk nok mange ganger, vil den relative frekvensen for et utfall nærme seg sannsynligheten for utfallet "

Dette er formuleringen  av  de store talls lov som læreboka bruker. I videoen, som du finner ved å åpne den følgende linken, vil du lære mer om hva denne loven går ut på.

Store talls lov virker sterkere og sterkere dess flere repetisjoner vi gjør av et forsøk. Dette har vi fått erfare ved å gjøre mange terningkast og samle dem i et eget regneark. Du kan åpne regnearket her. Sammenlign de relativ frekvensene som du oppnådde ved 100 repetisjoner med de relative frekvensene for hele klassen. Observerer du noen effekt av store talls lov?

Vi lærer i videoen hvordan vi kan simulere terningkast. Denne formelen kan du bruke for å simulure et terningskast: =TILFELDIGMELLOM(1,6). Skal du telle antall 2-ere, innenfor et område kan vi bruke kommandoen =ANTALL.HVIS(A3:A12;2). Hvis vi skal kopiere formelen til andre ruter, må vi bruke et dollartegn: $. Da blir formelen =ANTALL.HVIS($A$3:$A$12;2).

Fordelen med å simulere, er at vi kan få kastet mange flere kast på mye kortere tid enn om vi fysisk skulle gjøre det. Det kan være en nyttig øvelse å eksperimentere med dette.

1T-Illustrasjon av utvalgsrom

Videoen med denne tittelen finner du her. Du bør se i gjennom videoen før du leser denne teksten.

Utallige ganger har jeg, rett er at en oppgave et gitt, fått følgende spørsmål fra elever:

"Jeg forstår ikke denne oppgaven. Kan du hjelpe meg?" 

Jeg har mange ganger vært fristet til å svare: "Det gjør ikke jeg heller", og  det ville vært helt sant i mange tilfeller.  Mange oppgaver jeg forstår jeg ikke bare ved å lese teksten. Skal jeg løse makte å løse oppgaven, trenger jeg  en illustrasjon, men når illustrasjonen er ferdig, er oppgaven ofte så godt som løst.

I de oppgavene vi arbeider med i denne videoen, blir dette poenget godt illustrert. Lærer vi å bruke enkle redskaper som valgtre, krysstabell, diagrammer og oppramsinger, går oppgavene raskt fra å være uløselige eller vanskelige til å bli enkle. Vi må trene på slike teknikker for å bli flinke. Det er ikke noe annet å gjøre enn å løse mange oppgaver. Prøv gjerne å løse oppgavene uten å se på et eksempel eller løsning av en annen oppgave.

Oppgave 4.7 står igjen til deg. Ser du på ett av eksemplene, kan det være til stor hjelp. Oppgave 4.9 skal vi løse i forbindelse med en time.

Gi deg ikke med å løse de oppgavene som vi har løst sammen. Prøv deg på ukjente oppgaver som du finner bak i læreboka. Du kan være sikker på at ett av hjelpmidlene  oppramsing, krysstabell, diagrammer eller valgtre, vil forvandle oppgaven du strever med fra uforståelig og vanskelige til forståelige og løsbare.

   

R2-Algebraens fundamentalteorem

Videoen knyttet til dette emnet finner du her. Du bør se videoen før du leser denne teksten.

Algebraens fundamentalteorem er et av de viktigste teoremene(setningene) i matematikken. Det kobler sammen integralregning og derivasjon, og gjør at det å finne integraler blir mye enklere. Jeg markerer, i motsetning til læreboka,  betydningen av setningen  ved å benevne setningen med sitt egentlige navn. Navnet i seg selv forteller om betydningen som setningen har.

Min video bygger i hovedsak på Tom Lindstrøms bok Kalkulus, Universitetsforlaget 1996. Vi gjennomfører ikke et fullstendig bevis av setningen, men vi kommer et langt stykke på vei. Hvis du har lyst til å studere et fullstendig bevis av setningen, viser jeg til Lindstrøms bok.

Mine videoer dekker nå de tre første oppslagene av av dette kapitlet. Det er viktig at du får løst mange oppgaver. Listen over antideriverte er det svært viktig å memorere så raskt som mulig. Ganske raskt vil du måtte bruke disse funksjonene for å integrere nye og mer sammensatte funksjoner, og da vil du slite hvis ikke disse antideriverte er på plass.

R2-Bestemt integral

Videoen knyttet til dette emnet finner du her, og du bør se videoen før du går videre på denne teksten.

I denne videoen fortsetter vi å nærme oss integralbegrepet ved å bruke Oversummer og Undersummer. Her er GeoGebra er svært redskap fordi vi kan observere hva som skjer med oversummene og undersummene når vi øker antall rektangler over og  under funksjonsgrafen:

På figuren under har vi valgt n=4. Det betyr at vi får fram 4 par av rektangler. Forskjellen mellom Oversum og Undersum er her på 0.25.
Vi har brukt kommandoene SumOver[f,0,1,4] og SumUnder[f,0,1,4] for å fram disse rektanglene:



Setter er n=75, vil forskjellen bli mye mindre, bare 0.1. Det er vist på figuren under. Her har vi brukt kommandoene SumOver[f,0,1,75] og SumUnder[f,0,1,75]:


For å regne ut integralet direkte, bruker vi kommandoen Integral[f,0,1,4]. Bestemte integraler har en nedre og øvre grense. Dette skriver vi slik:

Vi får nå snart lønn for det møysommelige arbeidet vi har gjort så langt. Vi er svært nær en dypere forståelse av hva integral er for noe. Før vi kommer dit, er det viktig at du skaffer deg erfaring med å beregne oversummer og undersummer. Dette skal du både beherske ved å bruke håndredskaper og ved å bruke digitale hjelpemidler. Faren ved å bruke digitale hjelpemidler med en gang, er at resultatene kommer så enkelt og rakst at vi ikke får tid til å reflektere over det vi ser. Derfor bør du tvinge deg selv til mye håndarbeid.

Lykke til !